Grundschule

 Lemas

Die Grundschule Wasserburg wird SINUS – Schule

  1. Sinus an Grundschulen… So fing alles an:

     

Die Ergebnisse der TIMSS - Trends in International Mathematics and Science Study (1997) attestierte deutschen Schülern bei international vergleichenden Schulleistungsuntersuchungen nur das Mittelfeld. TIMSS - ist eine Studie, die seit 1995 im vierjährigen Turnus von der International Association for the Evaluation of Educational Achievement (IEA) durchgeführt wird. TIMSS untersucht Mathematik- und Naturwissenschaftsleistungen in der Grundschule, in der Sekundarstufe I und in der Sekundarstufe II.

Daraufhin initiierte die Bund-Länder-Kommission für Bildungsplanung und Forschungsförderung ein Programm auf der Grundlage des Gutachtens einer Expertengruppe unter der Leitung von Prof. Dr. Baumert –SINUS.

Das Programm »SINUS an Grundschulen« entwickelt den mathematischen und naturwissenschaftlichen Grundschulunterricht weiter. Es läuft von August 2009 bis Juli 2013. Zehn Länder der Bundesrepublik nehmen mit ausgewählten Grundschulen aktiv am Programm teil, fünf weitere Länder als assoziierte Mitglieder.

Lehrerinnen und Lehrer der Teilnehmergrundschulen arbeiten im Team an typischen Herausforderungen des Unterrichts. Sie richten ihren Blick auf die individuelle Förderung der Kinder und schaffen eine ausbaufähige Grundlage für das Lernen in der Sekundarstufe. Lehrkräfte dokumentieren und reflektieren ihre Arbeit und werden dabei vom Programmträger, dem Leibniz-Institut für die Pädagogik der Naturwissenschaften und Mathematik (IPN) wissenschaftlich begleitet.

 

  1. Allgemeine Informationen

 

Ziel
Das Sinus-Konzept vertritt für den Mathematikunterricht die konstruktivistische Grundposition. Das heißt Schüler lernen aktiv entdeckend und im sozialen Austausch. Lehrer nehmen ihre Aufgabe darin wahr, die Schüler als autonome aktiv Lernende zu unterstützen und ihr Lernen effizient zu moderieren. Das heißt, dass der Lernprozess der Schüler im Mittelpunkt steht. Dies schließt ein, dass Lehrer über das Potenzial der Lernenden in der spezifischen Lernumgebung Erfahrungen haben, um einschätzen zu können, was in einer bestimmten Arbeitssituation von den Lernenden als eigener Beitrag zu erwarten ist und wozu sie Unterstützung benötigen.
 

Leitlinien
Um den mathematischen Grundschulunterricht weiterzuentwickeln, will »SINUS an Grundschulen« die Zusammenarbeit von Lehrkräften fördern, denn gemeinsam lassen sich Unterrichtsveränderungen besser planen, umsetzen und beurteilen.
Lehrer nutzen zur eigenen Kompetenzentwicklung Anregungen und Unterstützung durch den Programmträger und andere Einrichtung. Es finden regelmäßige Treffen statt, bei denen gemeinsam Ziele festgelegt werden und Aufgaben klar verteilt werden. Bei diesen Treffen finden auch immer Unterrichtsmitschauen und kollegiale Hospitationen statt.
 

Arbeitsschwerpunkte
Teilnehmer des Programms »SINUS an Grundschulen« arbeiten mit einem Gerüst von zehn Modulen, in denen typische Problembereiche des Unterrichts beschrieben sind. Diese Module stammen aus dem Vorgängerprogramm SINUS-Transfer Grundschule und bilden weiterhin die Grundlage der Arbeit.

Basismodule
1 – Gute Aufgaben
2 – Entdecken, Erforschen, Erklären
3 – Schülervorstellungen aufgreifen

Aufbaumodule:
4 – Lernschwierigkeiten erkennen
5 – Talente entdecken
6 – Fachübergreifend lernen
7 – Interessen entwickeln
8 – Eigenständig und gemeinsam lernen
9 – Lernerfolg beurteilen
10 – Übergänge gestalten

Diese Positionen werden durch Gute Aufgaben und Lernumgebungen realisiert.
 

Kennzeichen:

Mathematische Kompetenzentwicklung
Gute Aufgaben/Lernumgebungen sollen zu einer umfassenden mathematischen Kompetenzentwicklung beitragen.

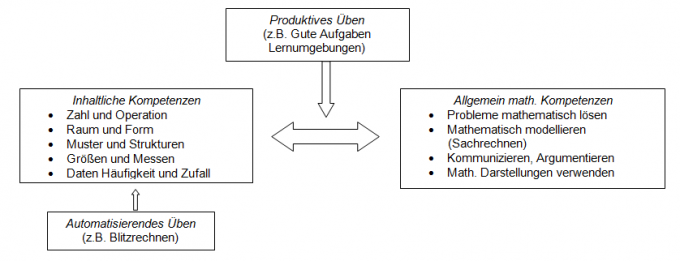
Zuerst sollen durch die Aufgabe Grundfertigkeiten (Inhaltliche Kompetenzen) geübt werden, die für die Klasse zurzeit besonders wichtig sind.
Dann soll die Aufgabe dem Schüler anbieten forschend - entdeckend und kreativ tätig zu werden. Der Schüler soll argumentieren und formulieren müssen und auch die Möglichkeit haben, die Aufgabe kooperativ mit anderen Schülern zu lösen (Allgemein mathematische Kompetenzen).

Strukturen und Beziehungen
Von Vorteil ist es weiterhin, wenn die Aufgabe eine Struktur besitzt, in der Beziehungen genutzt, thematisiert oder entdeckt werden können. Nicht zuletzt sollte die Aufgabe Variationsmöglichkeiten bieten, wenn sie eine gute Mathematikaufgabe sein will (Steinweg, A., 2006, S. 8-11).

Natürliche Differenzierung
Diese Übungsformen sind keineswegs nur für die starken Rechner gedacht: Vermuten, probieren, entdecken,... sind Lernziele für alle Kinder und für schwächere Rechner keineswegs weniger wichtig. Gerade offene Übungsformen sollen so gestaltet werden können, dass sie auf unterschiedlichen Anspruchniveaus einsetzbar sind.

Natürliche Differenzierung (nach Hengartner)

  • Schüler bestimmen selbst Anspruchsniveau
  • Geringes Einstiegsniveau
  • Nach oben offen
  • Sozialformen sind wichtig, ebenso Austausch und Reflexion
     
  1. Weitere interessante Informationen finden Sie unter folgenden Links:
     

Sinus an Grundschulen
Sinus-Grundschule

E-Paper: Die bayerische Grundschule